|
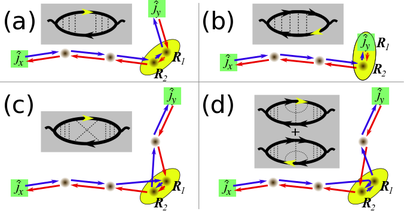
Fig: Diagrammatic and semiclassical representations of ex-trinsic contributions to the anomalous Hall conductance. [1]
|
The topological revolution of the end of the 2000ers promises the realization of robust quantum computing, nanoelectronics and ultraprecise optical sensing. All of these applications rely on the geometrical and topological properties of the quantum mechanical wave functions which are encoded in the Berry curvature and Berry phase.
In my research, I investigate the effect of impurity scattering on the quantum transport and optoelectronic response. Crucially, it appears that extrinsic scattering mechanisms can contribute to the same order as or even stronger than the intrinsic Berry curvature. Moreover, it turns out to be theoretically indispensible to incorporate impurity scattering beyond the relaxation time (i.e. non-crossing) approximation, see adjacent Figure. |
Recent Highlights:
|
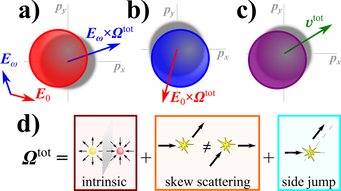
Fig: Physics of the gyrotropic Hall effect: a) [b)] Anomalous velocity of the ac [dc] field evaluated with the momentum shift due to the dc [ac] field. c) Contributions from non-linear dispersion. d) Intrinsic and extrinsic effects cumulate.
|
Gyrotropic Hall effect in Berry-curved materials [4]
We provide the first comprehensive study of the gyrotropic Hall effect, i.e. the non-linear ac Hall effect induced in time reversal invariant systems by a dc background current. Analyzing both intrinsic and extrinsic contributions, we demonstrate that the trace of the gyrotropic Hall tensor is determined by the number of Berry charges enclosed in the Fermi surface. It is thus substantial in topological semimetals but vanishing in non-topological matter and therefore a promising laboratory tool to discriminate topological from non-topological materials. |
|
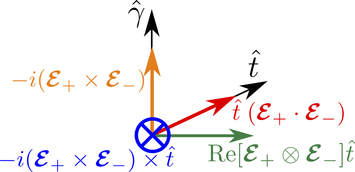
Fig: A tilt vector introduces a multitude of additional current directions in the photogalvanic effect of Weyl semimetals [3]
|
Photogalvanic effect in Weyl semimetals [3]
We demonstrate that an infinitesimal tilt can have multiple dramatic consequences on the photocurrent of Weyl semimetals. In particular, we show that skew scattering leads to additional current components and a strong linear photogalvanic effect, which competes with the shift current, appears. |
|
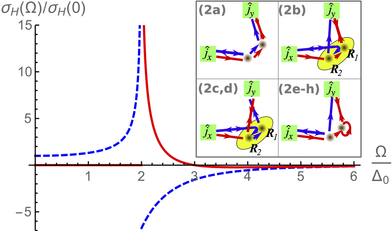
Fig: The ac Hall resistance for a single band 2D chiral p-wave superconductor is non-zero due to diffractive skew scattering. This determines the magnetooptical Kerr effect.
|
Kerr Effect from Diffractive Skew Scattering in Chiral px±ipy Superconductors [2]
We uncover a previously unnoticed mechanism for the Kerr effect in chiral p-wave superconductors. This mechanism is based on diffractive skew scattering and, crucially, also yields a non-zero Kerr response in the simplest model for a 2D chiral p-wave superconductor (a single parabolic band of spinless fermions), where all other mechanisms do not contribute. |
[6] L Powalla, J Kiemle, EJ König, et al. Nature Communications 13 (1), 1-8 (2022)
[5] EJ König, A Levchenko, Annals of Physics 435, 168492 (2021)
[4] EJ König, M Dzero, A Levchenko, DA Pesin, PRB 99, 155404 (2019)
[3] EJ König, HY Xie, DA Pesin, A Levchenko, PRB 96 (7), 075123 (2017)
[2] EJ König, A Levchenko, PRL 118 (2), 027001 (2017)
[1] EJ König, PM Ostrovsky, M Dzero, A Levchenko, PRB 94 (4), 041403 (R) (2016)
[5] EJ König, A Levchenko, Annals of Physics 435, 168492 (2021)
[4] EJ König, M Dzero, A Levchenko, DA Pesin, PRB 99, 155404 (2019)
[3] EJ König, HY Xie, DA Pesin, A Levchenko, PRB 96 (7), 075123 (2017)
[2] EJ König, A Levchenko, PRL 118 (2), 027001 (2017)
[1] EJ König, PM Ostrovsky, M Dzero, A Levchenko, PRB 94 (4), 041403 (R) (2016)